Ch4-Forward Kinematics
Summary:
- 运动学是后面计算雅克比和动力学的基础。
- 附录里简单比较了一下DH和PoE的区别,我也是因为PoE的优点才考虑学一学这套符号体系。
Production of Exponentials Formula(PoE)
和DH参数需要在每一个link都定义一个frame不同,PoE形式只需要定义我们关心的末端坐标系{b}和基座标系{s},或者我们也可以定义每一个link的frame:基坐标系{s}为{0},之后每个关节后的link都定义为{i},如果n个关节的话,末端还可以定义为{n+1}(或者直接认为{n}就是末端坐标系)
A. screw axes 在基坐标系下
PoE形式的核心想法是每一个joint都对它以下的所有link有一个screw运动,只要设置初始关节角为0,每个关节的正方向都确定之后,假设SE(3)下的M是一开始末端的坐标系相对于fixed base的构型。那么可以从最后一个关节反推到所有关节都有运动的末端变换矩阵:
\[T=e^{[S_1]\theta_1}...e^{[S_{n-1}]\theta_{n-1}}e^{[S_n]\theta_n}M\]因为都是相对于fixed base,所以都是对M或者子节点的变换矩阵左乘
注意:S一定是要在fixed frame下计算,M是初始的末端变换阵
例子
简单的例子就不举了,诀窍就在于每一个旋转轴都是按照基坐标系取,并且对应的线速度只考虑角速度和到基坐标系的外积(qxw = -[w]q)
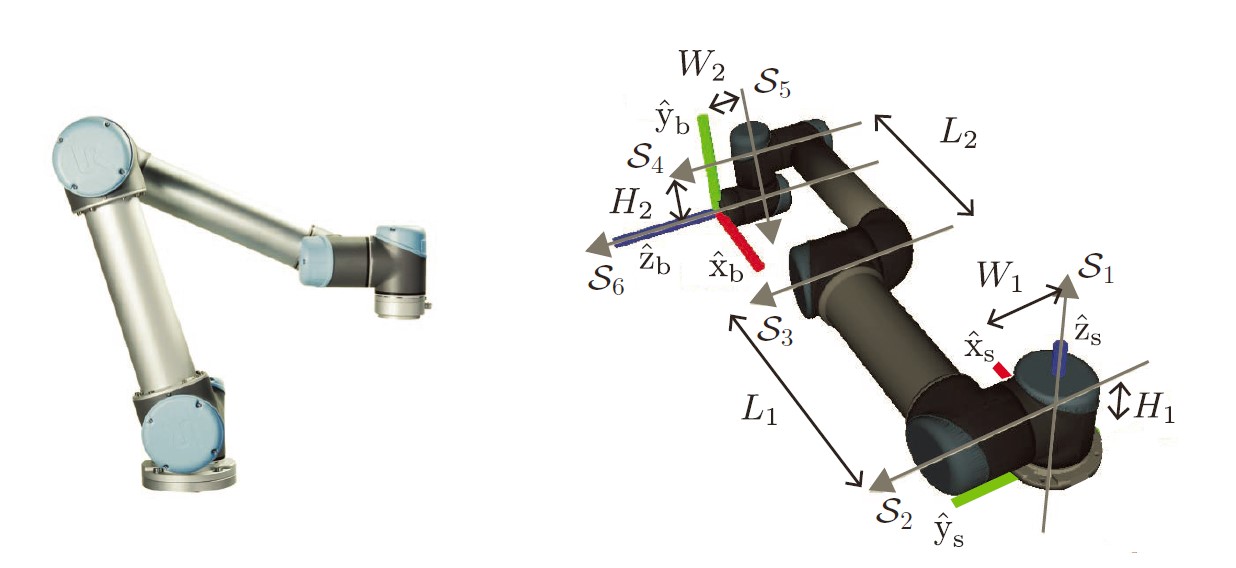
如图是非常经典的UR5臂的结构,用PoE的方法建模:
| i | \omega_i | v_i |
|---|---|---|
| 1 | (0, 0, 1) | (0, 0, 0) |
| 2 | (0, 1, 0) | (-H_1, 0, 0) |
| 3 | (0, 1, 0) | (-H_1, 0, L_1) |
| 4 | (0, 1, 0) | (-H_1, 0, L_1 + L_2) |
| 5 | (0, 0, -1) | (-W_1, L_1 +L_2, 0) |
| 6 | (0, 1, 0) | (H_2 - H_1, 0, L_1 + L_2) |
简单的说就是用右手定则,旋转角速度叉乘screw轴到base的线速度在base下的大小即为v_i的分量。
注意的是M的计算,其中R矩阵只需要用定义求就行({b}的每个轴用{s}表示)
\[T(\theta)=e^{[S_1]\theta_1}...e^{[S_{5}]\theta_{5}}e^{[S_6]\theta_6}M\]B. Screw Axes 在末端坐标系下
这里涉及到变换基坐标系,很容易想到上一章讲到的Adjoint 变换:
\[S_a=[Ad_{T_{ab}}]S_b\\ S_b^{i}= [Ad_{T_{bs}}]S_s^{i} = [Ad_{M^{-1}}]S_s^{i}\\ \to [S_b^{i}] = M^{-1}[S_s^{i}]{M^{-1}}^{-1}\]这里通过坐标系的变换,我们可以将T(\theta)表示为M在左侧的形式:
\[e^{M^{-1}PM} = M^{-1} e^{P} M\\ \to T(\theta)=e^{[S_1]\theta_1}...e^{[S_n]\theta_n}M\\ =e^{[S_1]\theta_1}...Me^{M^{-1}[S_n]M\theta_n}M^{-1}M \\ =Me^{M^{-1}[S_1]M\theta_1}M^{-1}...Me^{M^{-1}[S_{n-1}]M\theta_{n-1}}e^{M^{-1}[S_n]M\theta_n} \\ =Me^{M^{-1}[S_1]M\theta_1}...e^{M^{-1}[S_n]M\theta_n} \\ =Me^{[\mathcal{B}_1] \theta_1}...e^{[\mathcal{B}_n] \theta_n}\]最终相当于在body坐标系下从第一个关节开始不断地对M矩阵做右乘变换矩阵的操作,也就是相对初始的末端body坐标系下按照初始关节顺序和相对末端的旋转轴不断的变换。
比较space-form的公式和body-form公式:发现二者顺序的不同,并且S_i不受更远端的关节影响(只要从joint0到该关节构型固定,则S_i固定),类似的B_i不受更近端关节的影响。
正运动学由于有了之前的基础,变得异常的简单…em…是的
URDF(Universal Robot Description Format)
这算是个彩蛋?URDF在仿真中描述机器人的构型非常的有用,几乎包含了运动学和动力学所有需要的参数。
唯一的问题是URDF只能描述树状结构的机器人构型,对于闭链结构貌似无能为力,需要手动加dummy点。
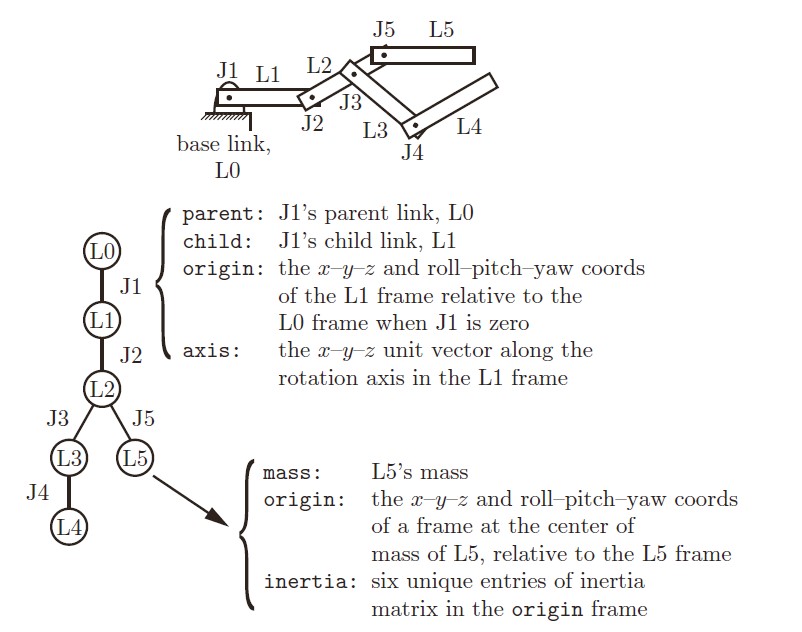
最后再来简单解释下实际的代码实现(以Matlab代码为例)
https://github.com/NxRLab/ModernRobotics
function T = FKinSpace(M, Slist, thetalist)
% *** CHAPTER 4: FORWARD KINEMATICS ***
% https://github.com/NxRLab/ModernRobotics
% Takes M: the home configuration (position and orientation) of the
% end-effector,
% Slist: The joint screw axes in the space frame when the manipulator
% is at the home position,
% thetalist: A list of joint coordinates.
% Returns T in SE(3) representing the end-effector frame, when the joints
% are at the specified coordinates (i.t.o Space Frame).
% Example Inputs:
%
% clear; clc;
% M = [[-1, 0, 0, 0]; [0, 1, 0, 6]; [0, 0, -1, 2]; [0, 0, 0, 1]];
% Slist = [[0; 0; 1; 4; 0; 0], ...
% [0; 0; 0; 0; 1; 0], ...
% [0; 0; -1; -6; 0; -0.1]];
% thetalist =[pi / 2; 3; pi];
% T = FKinSpace(M, Slist, thetalist)
%
% Output:
% T =
% -0.0000 1.0000 0 -5.0000
% 1.0000 0.0000 0 4.0000
% 0 0 -1.0000 1.6858
% 0 0 0 1.0000
T = M;
for i = size(thetalist): -1: 1
T = MatrixExp6(VecTose3(Slist(:, i) * thetalist(i))) * T;
end
end
VecTose3 实现比较简单,套用se(3)的定义就行
MatrixExp6的实现稍微复杂一点点,但仍然是定义,首先是把se3中的so3转化为twist,然后单位化得到axis的omegahat和theta,然后omegahat对应的[omegahat]只需要对so3单位化即可(除以theta),最后按照定义,拼成指数的结果T矩阵:
function T = MatrixExp6(se3mat)
% *** CHAPTER 3: RIGID-BODY MOTIONS ***
% Takes a se(3) representation of exponential coordinates.
% Returns a T matrix in SE(3) that is achieved by traveling along/about the
% screw axis S for a distance theta from an initial configuration T = I.
omgtheta = so3ToVec(se3mat(1: 3, 1: 3));
if NearZero(norm(omgtheta))
T = [eye(3), se3mat(1: 3, 4); 0, 0, 0, 1];
else
[omghat, theta] = AxisAng3(omgtheta);
omgmat = se3mat(1: 3, 1: 3) / theta;
T = [MatrixExp3(se3mat(1: 3, 1: 3)), ...
(eye(3) * theta + (1 - cos(theta)) * omgmat ...
+ (theta - sin(theta)) * omgmat * omgmat) ...
* se3mat(1: 3, 4) / theta;
0, 0, 0, 1];
end
end
MatrixExp3 就是求对应的R矩阵: 也是先求 “unit” screw axis
function R = MatrixExp3(so3mat)
% *** CHAPTER 3: RIGID-BODY MOTIONS ***
% Takes a 3x3 so(3) representation of exponential coordinates.
% Returns R in SO(3) that is achieved by rotating about omghat by theta
% from an initial orientation R = I.
omgtheta = so3ToVec(so3mat);
if NearZero(norm(omgtheta))
R = eye(3);
else
[omghat, theta] = AxisAng3(omgtheta);
omgmat = so3mat / theta;
R = eye(3) + sin(theta) * omgmat + (1 - cos(theta)) * omgmat * omgmat;
end
end
官方对变量名和对应的库函数有手册来解释:
https://github.com/NxRLab/ModernRobotics/blob/master/doc/MRlib.pdf