Modern Robotics: Ch6-Inverse Kinematics
Summary:
- 以串联机构的逆运动学为主,并联的运动学在Ch7会介绍。
- 串联的逆运动学通常是几何求解析(如果可行的话),对于无法求得解析解的构型考虑用梯度下降的迭代方法,目标函数采用指数积定义下当前末端和目标位姿的twist差。
- 对于速度的逆运动学,除了考虑伪逆的形式以外,还要根据关节的运动能力设置对应的cost function,比如整体动能和势能最小…
正运动学是给一组关节角,求末端的位姿(变换矩阵T)。
逆运动学是给定SE(3)空间下的位姿,求对应的关节角。(可能无解,也有可能有多解)
总的来说,这章的思想很简单,迭代法和解析法各有各的优点。解析或者几何法在推导过程中往往有着各种奇淫巧技(Tricky Method),但是对于一种构型的机器人,一般只需要推导一遍。而数值迭代法则有着思想明确,但是比较依赖初值的选取。
几何法
肉眼直观的解法,比解析法更加玄学的推导,依赖直觉和几何学,acos和atan2都比较常用。
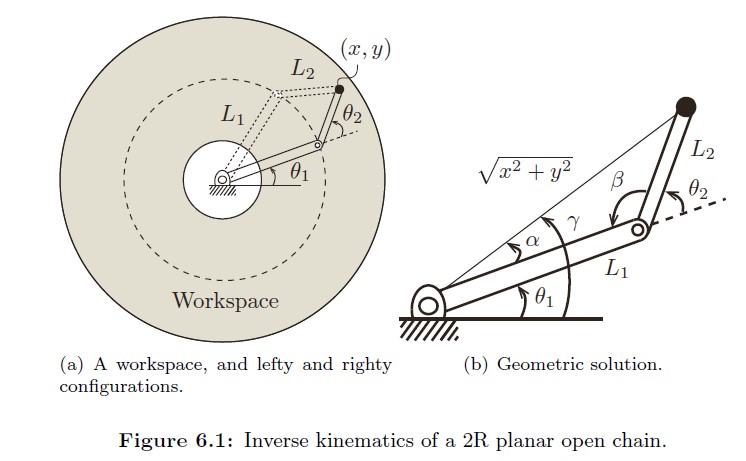
最简单的例子就比如这个2R平面连杆的IK,直接求对应的三角函数即可,当然对于多解会有选取的问题。
另外一个例子来自Kajita的Introduction to Humanoid Robotics
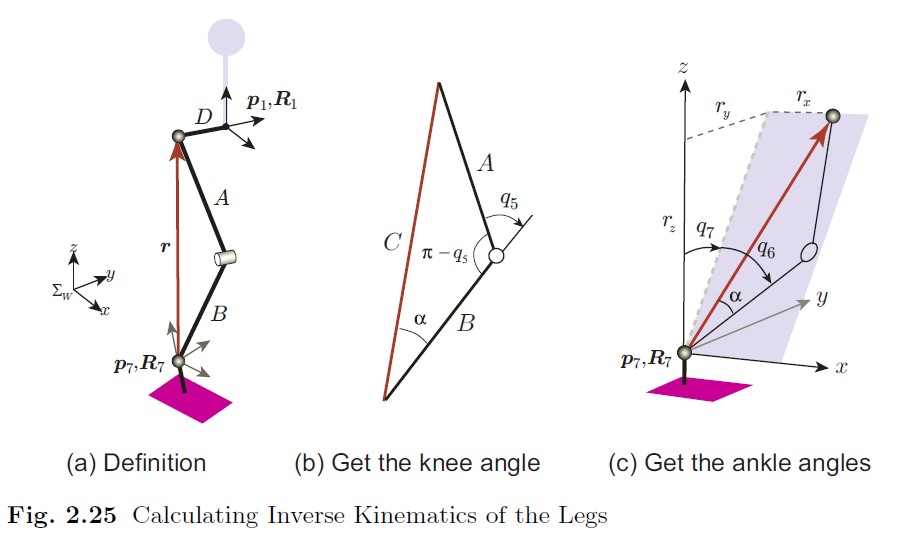
其中部分关节角通过几何法直接得到,另外比如q2,q3,q4则是通过解析法列等式求取。
解析法
解析法和几何法有相互借鉴的地方,往往是一起使用得到解析的答案,例如经典的YRPPPR(Y: Yaw, R: Roll, P: Pitch)构型,因为前三个关节角和最终的变换矩阵已知,那么最后三个关节(一般正交?方便列方程?)的角度往往可以用前已知量求得(一般都是将q1~q6最左边或者最右边的已知角度移动到右边),得到等式求解:
\[T_4T_5T_6=T_3^{-1}T_2^{-1}T_1^{-1} T^{6}_1 \\ e^{[\mathcal{S}_4]\theta_4}e^{[\mathcal{S}_5]\theta_5}e^{[\mathcal{S}_6]\theta_6} =e^{-[\mathcal{S}_3]\theta_3}e^{-[\mathcal{S}_2]\theta_2}e^{-[\mathcal{S}_1] \theta_1}XM^{-1}\]数值迭代法
一切都可以从牛顿寻根公式说起,对于一个已知的高次函数,寻找函数的跟往往没有解析解,那么只能通过初值加迭代的方法计算:
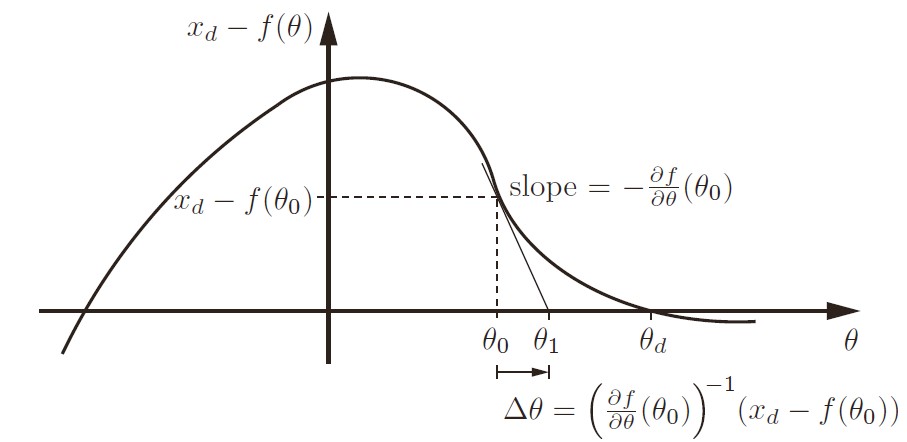
假设初值选取的离根的位置相对较近,那么总是可以通过泰勒展开得到:
\[x_d=f(\theta_d)=f(\theta_0)+ \underbrace{\left. \frac{\partial f}{\partial \theta}\right|\theta_0}_{J(\theta_0)} \underbrace{(\theta_d - \theta_0)}_{\Delta \theta}+ h. o. t.\]根据每次和期望的差,乘以Jacobian的逆,就能够计算角度的变化量:
\[\Delta \theta = J^{-1}(\theta_0)(x_d - f(\theta_0))\]这种方法的重点在于初值不能给的太随意,换句话说“对初值敏感”。**
另外一个问题是当Jacobian是不可逆的,这时候就需要做一些取舍,使用伪逆(或者其他形式的广义逆)
伪逆小知识1: MATLAB中通常x=A\b来求线性方程组,而不是x = pinv(A) * b,并且用LU分解的方式来做,速度会更快
伪逆小知识2:MP-pseudoinverse 在y有多解的时候是最小二范数解(右伪逆,J是扁矩阵, rank(J) > dimension, redundant),当线性方程组无解的时候代表队是误差平方和最小的解(左伪逆,J是高矩阵, rank(J) < dimension of end-effector, or singularity)
具体实现
- 给定目标位姿T,初始关节角\theta
- 计算当前位姿T_i和目标位姿T的误差 T_id,计算twist(log大法好!)
- 计算下一步的\theta_{i+1} = \theta_{i} + pinv(J) * twist_{id}
- i++
可以看到在位姿的误差上选取Twist作为参考,是非常科学的,(没有rpy欧拉角的耦合问题),Lynch老师如是说
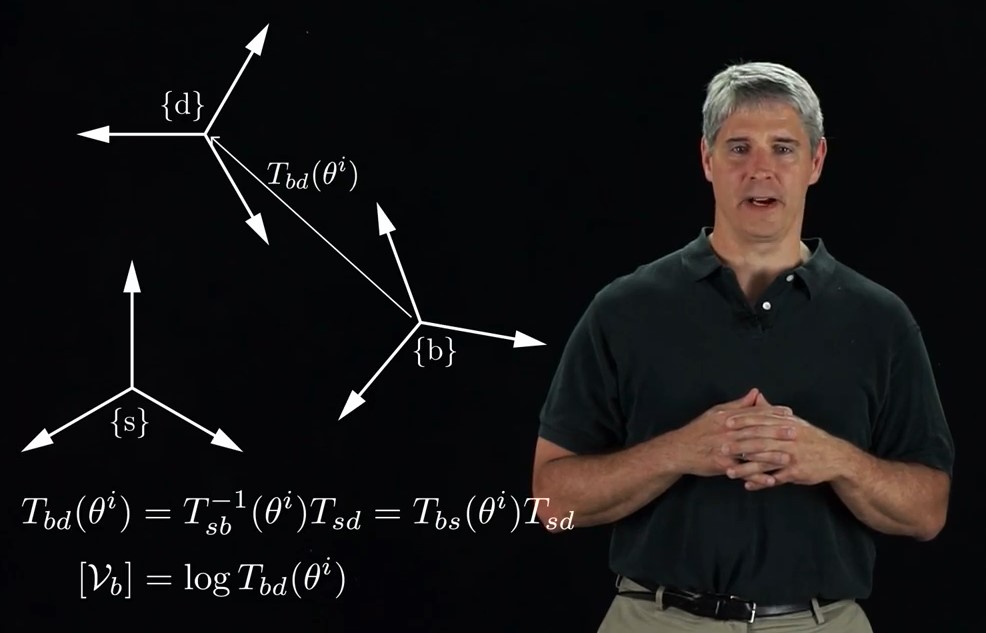
至于这里的计算细节就可以省略了,信任之前的库函数没有bug吧~
在实际的工程实现过程中,有时候当J不可逆,或者对伪逆不满意的时候,还有另外一种骚操作:对jacobian求转置作为逆代进去,本质上是做了个力的拖动,\tau = J^T F = J^T e(Twist) ,或者用优化的方法也能解释,但是这种情况收敛速度不会很快
逆运动学(速度),Inverse Velocity Kinematics
在运动规划过程中,我们除了给关节伺服发关节位置的指令外,最好还要有速度环和电流环(力矩)的前馈,关节速度的计算本质上还是运动学的问题:
位置微分
当然能够直接对两帧之间的位置做差分:
\[\dot{\theta} = (\theta_d(k\Delta t) - \theta_d((k-1) \Delta t)) / \Delta t\]这是可行的,当然差分的方法势必会带来噪声,需要对速度计算的响应速度和噪声之间做一个trade off
Jacobian计算
规划上通常是能够给出末端的运动速度的(twist或者是末端坐标系变化矩阵的时间函数),通过Jacobian的逆是可以得到关节角的速度:
\[\dot{\theta} = J^{+}(\theta) \mathcal{V}_d \\ \mathcal{V}_d(t) = T_{sd}^{-1}\dot{T}_{sd}(t)\]当关节是冗余的时候,此时用伪逆求出的关节角速度就是总速度平方和最小的情况。然而实际情况是不同关节的速度对应的惯量是不一样的,这样我们就可以对速度设置权重,对速度范围较小的关节设置较大的权重(比如用质量矩阵,或者再加上重力势能变化率最小)
\[min_{\dot{\theta}} {\frac{1}{2} \dot \theta ^T M(\theta) \dot{\theta} + \nabla h(\theta)^T \dot{\theta}} \\ s.t. ~~~J(\theta)\dot{\theta} = \mathcal{V}_d\]该优化问题有标准解法,设置拉格朗日系数,或者直接用KKT条件:

这里的重点在于优化出来的结果是有对应的物理意义:
\[J^T \lambda = M \dot{\theta}+\nabla h \\ \mathcal{V}_d=J\dot{\theta} \\ \to\\ \dot{\theta} = \underbrace{G \mathcal{V}_d}_{质量加权后的速度分量}+\underbrace{(I-GJ)M^{-1}\nabla{h}}_{势能加权后的速度分量} \\ \underbrace{\lambda}_{末端的等效wrench}=\underbrace{B \mathcal{V}_d}_{拖动末端运动的等效动态力} + \underbrace{BJM^{-1}\nabla{h}}_{重力补偿的力} \\ B=(JM^{-1}J^{T})^{-1} \\ G=M^{-1}J^T(JM^{-1}J^T)^{-1}=M^{-1}J^TB\]尤其是当不考虑势能,或者势能为0时,对应的角速度就是GV,G矩阵就是根据质量矩阵加权的权重矩阵。
这里末端等效力和末端等效质量矩阵在Ch8会详细介绍
编程
这里留地方给之后尝试KDL和其他一些运动学的库的链接。