Denavit Hartenberg Para
Summary:
- 澄清一些概念,理清一些思路,最近看7DoF 逆运动学算法的Paper又掉DH参数的坑里了
- Matlab的Robotics toolbox 真香,真好用!
DH参数
这篇文章用的是标准的DH参数,标准型和改进型的区别参见:
https://blog.csdn.net/qq_27170195/article/details/79936518
DH将一个齐次变换拆成了四个body frame的连续变换(右乘),前提是坐标系x轴和另一个的z轴垂直相交。
(4个参数+距离定义蕴含的垂直关系(2个)其实也是6个自由度。)
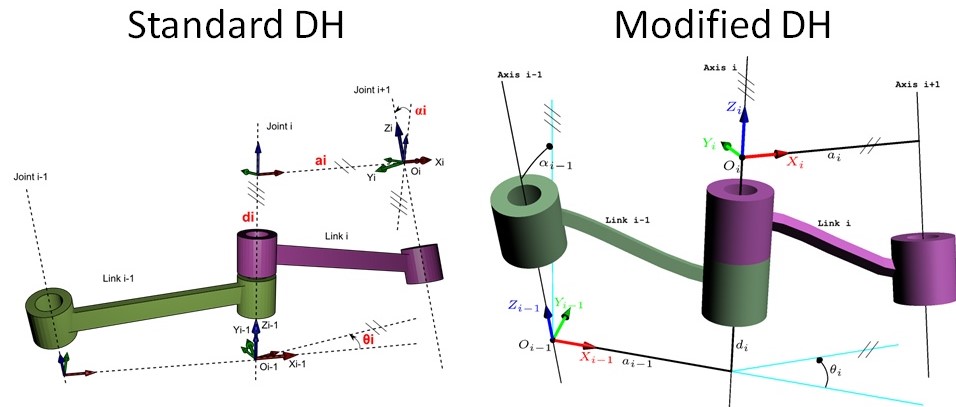
STD_DH: \(T_{n-1,n}= ^{n-1} T_{n}=\left(\operatorname{Trans}_{z_{n-1}}\left(d_{n}\right) \cdot \operatorname{Rot}_{z_{n-1}}\left(\theta_{n}\right)\right) \cdot \left(\operatorname{Trans}_{x_{n}}\left(a_{n}\right) \cdot \operatorname{Rot}_{x_{n}}\left(\alpha_{n}\right) \right)\\ = \left[\begin{array}{cccc}{\cos \theta_{i}} & {-\sin \theta_{i} \cos \alpha_{i}} & {\sin \theta_{i} \sin \alpha_{i}} & {a_{i} \cos \theta_{i}} \\ {\sin \theta_{i}} & {\cos \theta_{i} \cos \alpha_{i}} & {-\cos \theta_{i} \sin \alpha_{i}} & {a_{i} \sin \theta_{i}} \\ {0} & {\sin \alpha_{i}} & {\cos \alpha_{i}} & {d_{i}} \\ {0} & {0} & {0} & {1}\end{array}\right]\) MOD_DH: \(T_{n-1,n} = ^{n-1}T_{n}=\left(\operatorname{Rot}_{x_{n-1}}\left(\alpha_{n-1}\right) \cdot \operatorname{Trans}_{x_{n-1}}\left(a_{n-1}\right)\right) \cdot \left(\operatorname{Rot}_{z_{n}}\left(\theta_{n}\right) \cdot \operatorname{Trans}_{z_{n}}\left(d_{n}\right)\right) \\=\left[\begin{array}{cccc}{\cos \theta_{i}} & {-\sin \theta_{i}} & {0} & {a_{i-1}} \\ {\sin \theta_{i} \cos \alpha_{i-1}} & {\cos \theta_{i} \cos \alpha_{i-1}} & {-\sin \alpha_{i-1}} & {-d_{i} \sin \alpha_{i-1}} \\ {\sin \theta_{i} \sin \alpha_{i-1}} & {\cos \theta_{i} \sin \alpha_{i-1}} & {\cos \alpha_{i-1}} & {d_{i} \cos \alpha_{i-1}} \\ {0} & {0} & {0} & {1}\end{array}\right]\)
主要区别在于Link的固连坐标系(标准的选在下一个关节的坐标系,而改进的选在上一个关节的坐标系)
同时DH方法在关节坐标系上的选取也比较特殊(看例子就知道,关节轴并不一定和实际AXIS轴重合,保证平行)
Matlab自带的RigidBodyTree支持TransformMatrix也支持DH/MDH
setFixedTransform(jointObj,tform) sets the JointToParentTransform property of the Jointobject directly with the supplied homogenous transformation.
setFixedTransform(jointObj,dhparams,"dh") sets the ChildToJointTransform property using Denavit-Hartenberg (DH) parameters. The JointToParentTransform **property is set to an **identity matrix. DH parameters are given in the order [a alpha d theta].
The theta input is ignored when specifying the fixed transformation between joints because that angle is dependent on the joint configuration. For more information, see Rigid Body Tree Robot Model.
setFixedTransform(jointObj,mdhparams,"mdh") sets the JointToParentTransform property using modified DH parameters. The ChildToJointTransform property is set to an identity matrix. Modified DH parameters are given in the order [a alpha d theta].
https://blog.csdn.net/Herr_ji/article/details/97933740
https://blog.csdn.net/weixin_39090239/article/details/82153333
小实验
- STD DH
dhparams = [0 -pi/2 0.35 0;
0 pi/2 0.0 0;
0 -pi/2 0.4 0;
0 pi/2 0 0;
0 -pi/2 0.5 0;
0 pi/2 0 0;
0 0 0.1 0];
iiwa_DH = robotics.RigidBodyTree;
body1 = robotics.RigidBody('body1');
jnt1 = robotics.Joint('jnt1','revolute');
setFixedTransform(jnt1,dhparams(1,:),'dh');
body1.Joint = jnt1;
addBody(iiwa_DH,body1,'base')
body2 = robotics.RigidBody('body2');
jnt2 = robotics.Joint('jnt2','revolute');
body3 = robotics.RigidBody('body3');
jnt3 = robotics.Joint('jnt3','revolute');
body4 = robotics.RigidBody('body4');
jnt4 = robotics.Joint('jnt4','revolute');
body5 = robotics.RigidBody('body5');
jnt5 = robotics.Joint('jnt5','revolute');
body6 = robotics.RigidBody('body6');
jnt6 = robotics.Joint('jnt6','revolute');
body7 = robotics.RigidBody('body7');
jnt7 = robotics.Joint('jnt7','revolute');
setFixedTransform(jnt2,dhparams(2,:),'dh');
setFixedTransform(jnt3,dhparams(3,:),'dh');
setFixedTransform(jnt4,dhparams(4,:),'dh');
setFixedTransform(jnt5,dhparams(5,:),'dh');
setFixedTransform(jnt6,dhparams(6,:),'dh');
setFixedTransform(jnt7,dhparams(7,:),'dh');
body2.Joint = jnt2;
body3.Joint = jnt3;
body4.Joint = jnt4;
body5.Joint = jnt5;
body6.Joint = jnt6;
body7.Joint = jnt7;
addBody(iiwa_DH,body2,'body1')
addBody(iiwa_DH,body3,'body2')
addBody(iiwa_DH,body4,'body3')
addBody(iiwa_DH,body5,'body4')
addBody(iiwa_DH,body6,'body5')
addBody(iiwa_DH,body7,'body6')
figure;
% config = randomConfiguration(iiwa_DH)
% show(iiwa_DH,config)
show(iiwa_DH);
- Mod_DH

dhparams = [0 0 0.35 0;
0 -pi/2 0.0 0;
0 pi/2 0.4 0;
0 -pi/2 0 0;
0 pi/2 0.5 0;
0 -pi/2 0 0;
0 pi/2 0.1 0];
iiwa_MDH = robotics.RigidBodyTree;
body1 = robotics.RigidBody('body1');
jnt1 = robotics.Joint('jnt1','revolute');
setFixedTransform(jnt1,dhparams(1,:),'mdh');
body1.Joint = jnt1;
addBody(iiwa_MDH,body1,'base')
body2 = robotics.RigidBody('body2');
jnt2 = robotics.Joint('jnt2','revolute');
body3 = robotics.RigidBody('body3');
jnt3 = robotics.Joint('jnt3','revolute');
body4 = robotics.RigidBody('body4');
jnt4 = robotics.Joint('jnt4','revolute');
body5 = robotics.RigidBody('body5');
jnt5 = robotics.Joint('jnt5','revolute');
body6 = robotics.RigidBody('body6');
jnt6 = robotics.Joint('jnt6','revolute');
body7 = robotics.RigidBody('body7');
jnt7 = robotics.Joint('jnt7','revolute');
setFixedTransform(jnt2,dhparams(2,:),'mdh');
setFixedTransform(jnt3,dhparams(3,:),'mdh');
setFixedTransform(jnt4,dhparams(4,:),'mdh');
setFixedTransform(jnt5,dhparams(5,:),'mdh');
setFixedTransform(jnt6,dhparams(6,:),'mdh');
setFixedTransform(jnt7,dhparams(7,:),'mdh');
body2.Joint = jnt2;
body3.Joint = jnt3;
body4.Joint = jnt4;
body5.Joint = jnt5;
body6.Joint = jnt6;
body7.Joint = jnt7;
addBody(iiwa_MDH,body2,'body1')
addBody(iiwa_MDH,body3,'body2')
addBody(iiwa_MDH,body4,'body3')
addBody(iiwa_MDH,body5,'body4')
addBody(iiwa_MDH,body6,'body5')
addBody(iiwa_MDH,body7,'body6')
figure;
show(iiwa_MDH);
二者只是在link选择的Joint坐标系序号不同而已,只不过在Joint坐标系选取的时候考虑到DH的特殊性约束。
- Axis(urdf导入)
robot = importrobot('iiwa14.urdf');
robot.show('visuals','off');
urdf的建模思路是先建立Link(包括各个link质心(相对link原点),惯量(相对于质心)),然后建立Joint的坐标系,相对于上一个Joint的变换(xyz,rpy),一般默认将axis放在z轴,当然也可以不标准。
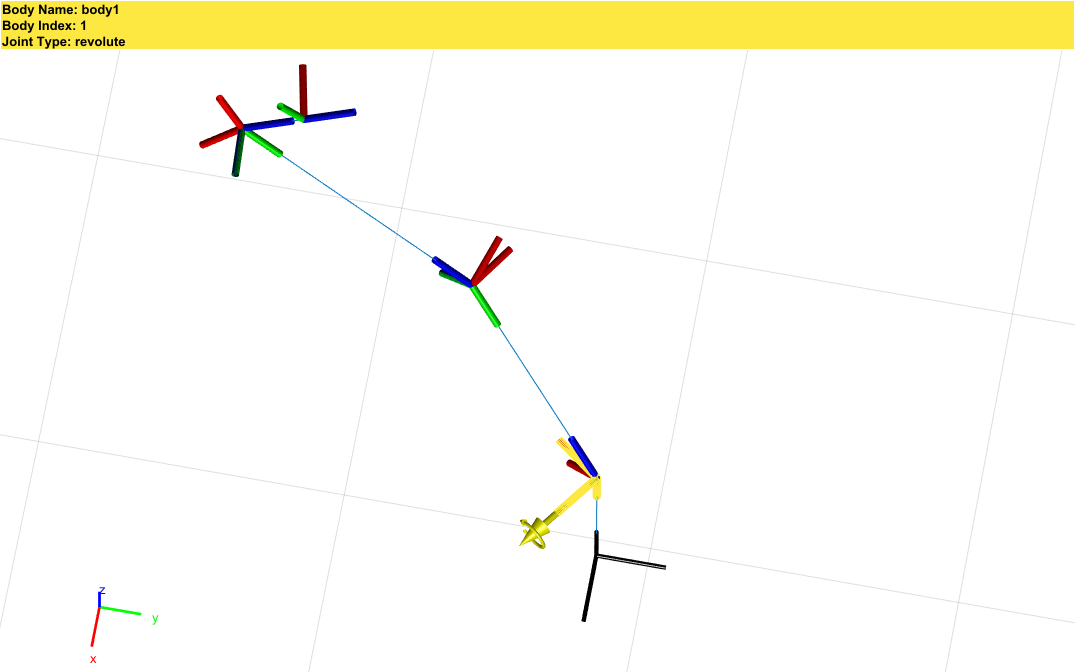
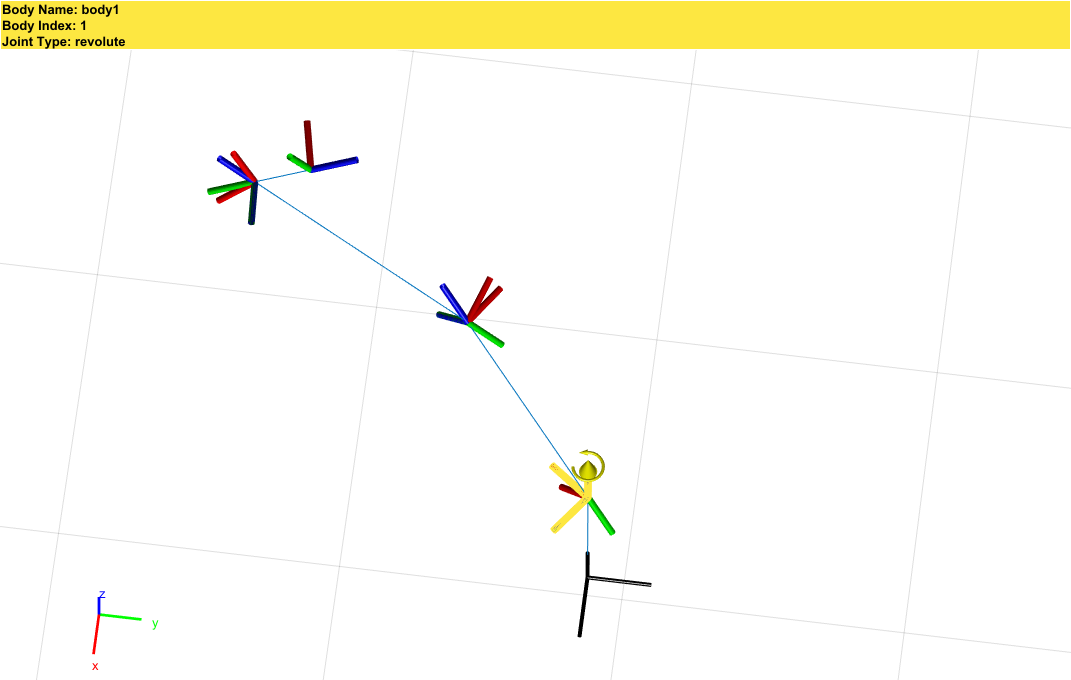
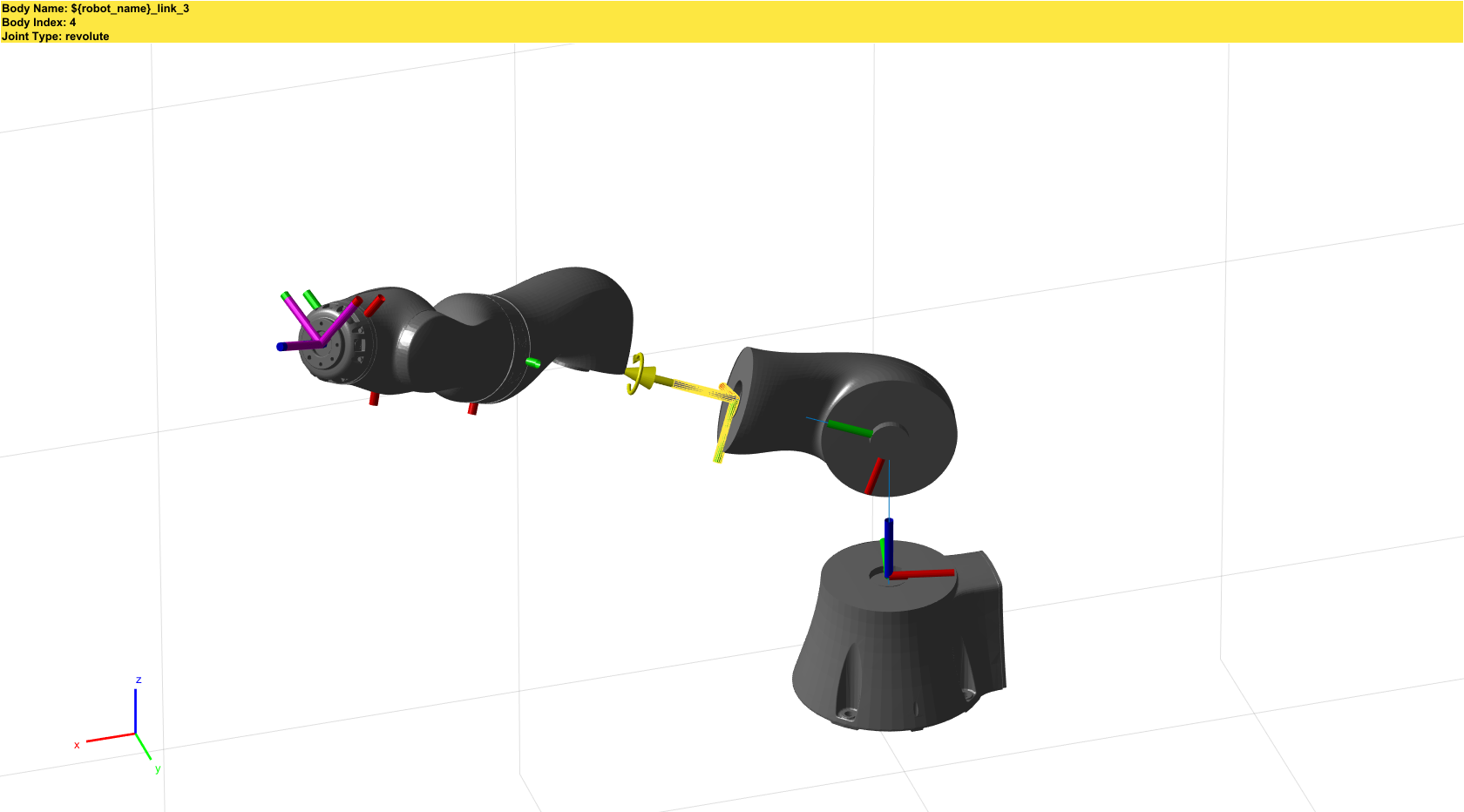
并且DH参数选定的Link坐标和Joint坐标会比较奇怪?比如三关节的Joint坐标并不在三关节上?
(参见上图比较就能得知~用DH参数貌似真的只是时代的限制?)
(DH的优点在于参数少到只有4个就能够表述机器人当前的构型,但是会存在无法确定机器人实际关节位置和正方向的问题)
而普通的Joint2Joint的Transform变换,虽然用齐次变换矩阵(但是理论上rpy+xyz也是只需要6个参数?)
貌似DH参数满足参数最小原理,通常用在校准上(末端5点法校正参数,以及4点法最小二乘计算TCP位置),用校正完的DH参数能减小末端的轨迹误差(处理link和Joint在装配上的问题)绝对定位精度!
【关于机器人20点标定的原理? 】 https://www.zhihu.com/question/54682285/answer/336365316
DH缺点在于当连续两个joint平行时,一点点的装配误差会导致坐标轴X出现较大的变化。
【为什么 DH 建模方法存在奇异性,而指数积方法没有奇异性?】 https://www.zhihu.com/question/60052059/answer/536713760
一台新组装出来的机器人在出厂之前,如果没有经过一系列的参数校准也许会有较好的重复定位精度(precision),然而定位准确度和轨迹跟踪准确度(accuracy)却很差。对于一些固定重复性的搬运工作,重复定位精度是重要考量,可能对绝对定位准确度也没有要求,对于这一类应用场景来说,机器人标定似乎不是必须的。然而对于有些应用场景,较高的定位准确度和轨迹跟踪能力是任务成功完成的关键,比如如动态拾捡,焊接,涂胶,机械臂视觉工件尺寸检测,上下料,机加工等。对于这一类应用场景,机器人标定是出厂前的必须工作。
校准内容:
机器人参数校准本质是其数学模型与物理参数“对准”的过程,总体来讲校准的层次可分为三层:
层次一,关节校准:校准关节位置偏移(关节寻零);
层次二,几何尺寸校准:校准关节间的相对位姿(DH参数和传动参数);
层次三,动力学参数校准:关节质量,惯量,摩擦,刚性等。
后续
基于Mordern robotics 的mr_lib可以根据机器人的质量惯量参数计算ID,这部分也可以用Matlab的rigidbodytree的函数来验证。MATLAB真的强:1st_place_medal:
robot = importrobot('iiwa14.urdf');
figure(1);
robot.show('visuals','off');
robot.DataFormat = 'row';
robot.Gravity = [0 0 -9.81];
q = [0,pi / 3,0, 0, 0, pi/2 ,0];
gtau = gravityTorque(robot,q)
>> showdetails(robot)
--------------------
Robot: (9 bodies)
Idx Body Name Joint Name Joint Type Parent Name(Idx) Children Name(s)
--- --------- ---------- ---------- ---------------- ----------------
1 ${robot_name}_link_0 world_desk${robot_name}_joint fixed world_desk(0) ${robot_name}_link_1(2)
2 ${robot_name}_link_1 ${robot_name}_joint_1 revolute ${robot_name}_link_0(1) ${robot_name}_link_2(3)
3 ${robot_name}_link_2 ${robot_name}_joint_2 revolute ${robot_name}_link_1(2) ${robot_name}_link_3(4)
4 ${robot_name}_link_3 ${robot_name}_joint_3 revolute ${robot_name}_link_2(3) ${robot_name}_link_4(5)
5 ${robot_name}_link_4 ${robot_name}_joint_4 revolute ${robot_name}_link_3(4) ${robot_name}_link_5(6)
6 ${robot_name}_link_5 ${robot_name}_joint_5 revolute ${robot_name}_link_4(5) ${robot_name}_link_6(7)
7 ${robot_name}_link_6 ${robot_name}_joint_6 revolute ${robot_name}_link_5(6) ${robot_name}_link_7(8)
8 ${robot_name}_link_7 ${robot_name}_joint_7 revolute ${robot_name}_link_6(7) ${robot_name}_link_ee(9)
9 ${robot_name}_link_ee ${robot_name}_joint_ee fixed ${robot_name}_link_7(8)
--------------------
>> gtau
gtau =
-0.0000 -46.3066 -0.3125 12.5887 -0.2972 -0.1539 0