Simple Demo of Inverse Dynamics
本质上逆动力学就是个给定关节状态(q,qDot,qDDot),计算关节力矩的过程:
考虑到计算复杂度的关系,牛顿-欧拉迭代方法最适合计算器(机)程序来执行。
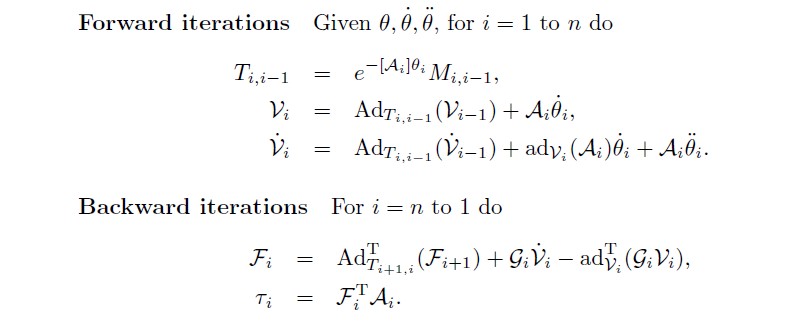
大致流程都相同,FeatherStone在正向过程中会先计算部分的连杆间作用力,然后再叠加子连杆对父连杆的作用力。当然也可以一起放到反向迭代中将连杆间作用力和连杆本身的惯性力一起计算。
MATLAB Toolbox
Matlab Robotics Toolbox支持导入urdf和DH参数等建模方式,支持正逆运动学和动力学解算。
可以作为验证方式之一。
https://ww2.mathworks.cn/products/robotics.html
2019b的Robotics System Toolbox从2018b的v2.1升级到了3.0,具体各个版本之间的Feature参见
https://ww2.mathworks.cn/help/robotics/release-notes.html
最早R2016b支持ROS接口时就明白万能的MATLAB在Robotics上也会插一脚的,导入STL的可视化从R2017b开始能够使用,而动力学部分的计算则从R2018a开始提供。最新的R2019b支持碰撞检测算法以及一些商用版本的机械臂的模型(虽然开源途径也很方便拿?)看了一眼资源文件:
..\R2019b\toolbox\robotics\robotmanip\data\roboturdf,大概所有的urdf直接是从ROS那边拷贝过来的。
也就是说,利用MATLAB的RoboticsToolBox+urdf+mesh资源,我们可以在MATLAB里实现rViz的可视化功能+rbdl的动力学计算功能。
有时间也可以试试19b新出的Collision Check函数,感觉学术上作为验算包是足够了。
针对iiwa14的动力学测试代码:
robot = importrobot('iiwa14.urdf');
robot.DataFormat = 'row';
robot.Gravity = [0 0 -9.81];
thetalist = [0.234, 0.543, 0.32, 0.521, 1.32, 1.75, 1.2];
qDot = [0.8828 0.9137 0.5583 0.5989 0.1489 0.8997 0.4504] * 30;
qDDot = [0.9718 0.9880 0.8641 0.3889 0.4547 0.2467 0.7844] * 30;
invTau = inverseDynamics(robot,thetalist,qDot,qDDot);
vpa(invTau,4)
输出结果:
[ 1173.0, 28.58, -384.5, -203.5, 14.14, 8.318, -0.7227]
Modern Robotics code (mr_lib)
按照Lynch教材中的符号定义,以及官网给出的开源matlab代码,可以轻松搞定一系列计算。
前提是计算好Slist, Mlist和Glist.
这里主要的坑在于惯性矩阵(Spatial Inertial Matrix)的计算,urdf默认的惯性张量是相对于质心的,而Screw的方法一般将link的坐标系建立在前端关节上,需要在计算Inertia和Glist的时候做一个转换:
惯性张量由于是3*3的矩阵,直接按照平移定理,q和b坐标系平行,q在{b}系的坐标为q(列向量)
\[\mathcal{I}_{q}=\mathcal{I}_{b}+\mathfrak{m}\left(q^{\mathrm{T}} q I-q q^{\mathrm{T}}\right)\]而Spatial Inertial的坐标变换则需要用到adjoint变换(这里同样只是平移,R=eye(3)):
\[\mathcal{G}_{a}=\left[\operatorname{Ad}_{T_{b a}}\right]^{\mathrm{T}} \mathcal{G}_{b}\left[\operatorname{Ad}_{T_{b a}}\right] \\= \left[\begin{array}{cc}{R} & {0} \\ {[p] R} & {R}\end{array}\right]^T\mathcal{G}_{b}\left[\begin{array}{cc}{R} & {0} \\ {[p] R} & {R}\end{array}\right] \\=\left[\begin{array}{cc}{\mathcal{I}_{b}} & {[p]^{T}\cdot mI_{3\times3}} \\ {m{I}_{3\times3}\cdot [p]} & {mI_{3\times3}}\end{array}\right]\]利用mr_lib的matlab脚本:
j1_rpy = [0, 0 , 0]; j1_xyz = [0,0, 0.1575]';
j2_rpy = [pi/2, 0 , pi]; j2_xyz = [0,0, 0.2025]';
j3_rpy = [pi/2, 0 , pi]; j3_xyz = [0,0.2045, 0]';
j4_rpy = [pi/2, 0 , 0]; j4_xyz = [0,0, 0.2155]';
j5_rpy = [-pi/2, pi , 0]; j5_xyz = [0,0.1845, 0]';
j6_rpy = [pi/2, 0 , 0]; j6_xyz = [0,0, 0.2155]';
j7_rpy = [-pi/2, pi , 0]; j7_xyz = [0,0.0810, 0]';
Mass = [4, 4, 3, 2.7, 1.7, 1.8, 0.3];
L1_m_xyz = [0 -0.03 0.12]'; L1_inertia = diag([0.1,0.09,0.02]);
L2_m_xyz = [0.0003 0.059 0.042]'; L2_inertia = diag([0.05,0.018,0.044]);
L3_m_xyz = [0 0.03 0.13]'; L3_inertia = diag([0.08,0.075,0.01]);
L4_m_xyz = [0 0.067 0.034]'; L4_inertia = diag([0.03,0.01,0.029]);
L5_m_xyz = [0.0001 0.021 0.076]'; L5_inertia = diag([0.02,0.018,0.005]);
L6_m_xyz = [0 0.0006 0.0004]'; L6_inertia = diag([0.005,0.0036,0.0047]);
L7_m_xyz = [0 0 0.02]'; L7_inertia = diag([0.001,0.001,0.001]);
L1_inertia = L1_inertia + Mass(1) * ( L1_m_xyz' * L1_m_xyz * eye(3) - L1_m_xyz * L1_m_xyz');
L2_inertia = L2_inertia + Mass(2) * ( L2_m_xyz' * L2_m_xyz * eye(3) - L2_m_xyz * L2_m_xyz');
L3_inertia = L3_inertia + Mass(3) * ( L3_m_xyz' * L3_m_xyz * eye(3) - L3_m_xyz * L3_m_xyz');
L4_inertia = L4_inertia + Mass(4) * ( L4_m_xyz' * L4_m_xyz * eye(3) - L4_m_xyz * L4_m_xyz');
L5_inertia = L5_inertia + Mass(5) * ( L5_m_xyz' * L5_m_xyz * eye(3) - L5_m_xyz * L5_m_xyz');
L6_inertia = L6_inertia + Mass(6) * ( L6_m_xyz' * L6_m_xyz * eye(3) - L6_m_xyz * L6_m_xyz');
L7_inertia = L7_inertia + Mass(7) * ( L7_m_xyz' * L7_m_xyz * eye(3) - L7_m_xyz * L7_m_xyz');
M01 = [eul2rotm([j1_rpy(3),j1_rpy(2),j1_rpy(1)],'ZYX'),j1_xyz; 0,0,0,1];
M12 = [eul2rotm([j2_rpy(3),j2_rpy(2),j2_rpy(1)],'ZYX'),j2_xyz; 0,0,0,1];
M23 = [eul2rotm([j3_rpy(3),j3_rpy(2),j3_rpy(1)],'ZYX'),j3_xyz; 0,0,0,1];
M34 = [eul2rotm([j4_rpy(3),j4_rpy(2),j4_rpy(1)],'ZYX'),j4_xyz; 0,0,0,1];
M45 = [eul2rotm([j5_rpy(3),j5_rpy(2),j5_rpy(1)],'ZYX'),j5_xyz; 0,0,0,1];
M56 = [eul2rotm([j6_rpy(3),j6_rpy(2),j6_rpy(1)],'ZYX'),j6_xyz; 0,0,0,1];
M67 = [eul2rotm([j7_rpy(3),j7_rpy(2),j7_rpy(1)],'ZYX'),j7_xyz; 0,0,0,1];
M7e = [eye(3),[0;0;0.045]; 0,0,0,1];
Mlist = cat(3, M01,M12,M23,M34,M45,M56,M67,M7e);
G1 = [L1_inertia, VecToso3(L1_m_xyz) * Mass(1); VecToso3(L1_m_xyz)' * Mass(1),eye(3) * Mass(1)];
G2 = [L2_inertia, VecToso3(L2_m_xyz) * Mass(2); VecToso3(L2_m_xyz)' * Mass(2),eye(3) * Mass(2)];
G3 = [L3_inertia, VecToso3(L3_m_xyz) * Mass(3); VecToso3(L3_m_xyz)' * Mass(3),eye(3) * Mass(3)];
G4 = [L4_inertia, VecToso3(L4_m_xyz) * Mass(4); VecToso3(L4_m_xyz)' * Mass(4),eye(3) * Mass(4)];
G5 = [L5_inertia, VecToso3(L5_m_xyz) * Mass(5); VecToso3(L5_m_xyz)' * Mass(5),eye(3) * Mass(5)];
G6 = [L6_inertia, VecToso3(L6_m_xyz) * Mass(6); VecToso3(L6_m_xyz)' * Mass(6),eye(3) * Mass(6)];
G7 = [L7_inertia, VecToso3(L7_m_xyz) * Mass(7); VecToso3(L7_m_xyz)' * Mass(7),eye(3) * Mass(7)];
Glist = cat(3, G1,G2,G3,G4,G5,G6,G7);
Slist = [ [0;0;1;0;0;0], [0;1;0;-(j2_xyz(3) +j1_xyz(3));0;0], [0;0;1;0;0;0], ...
[0;-1;0; (j4_xyz(3) +j3_xyz(2) + j2_xyz(3) +j1_xyz(3)); 0;0], ...
[0;0;1;0;0;0], [0;1;0; - (j6_xyz(3) +j5_xyz(2) + j4_xyz(3) +j3_xyz(2) + j2_xyz(3) +j1_xyz(3));0;0], ...
[0;0;1;0;0;0]];
g = [0,0,-9.81]';
thetalist = [0.234, 0.543, 0.32, 0.521, 1.32, 1.75, 1.2]';
dthetalist = [0.8828 0.9137 0.5583 0.5989 0.1489 0.8997 0.4504] * 30;
ddthetalist = [0.9718 0.9880 0.8641 0.3889 0.4547 0.2467 0.7844] * 30;
tau = InverseDynamics(thetalist, dthetalist, ddthetalist ,g, ...
[0; 0; 0; 0; 0; 0], Mlist, Glist, Slist)';
vpa(tau,4)
输出:
[ 1173.0, 28.6, -384.5, -203.6, 14.13, 8.318, -0.7227]
Rigid Body Dynamic Library
RBDL库是按照FeatherStone的教材符号编写的动力学计算库(我用的C++版本,当然也有python的Wrapper)
唯一的坑在于传入SpatialTransform的姿态矩阵不是转移矩阵而是从父坐标系到子坐标系的变换矩阵(正好需要求逆或者转置),作为C++版本,代码还是非常值得学习的。
https://bitbucket.org/rbdl/rbdl/issues/96/transpose-in-spatialtransform-operator
Martin Felis:
I am following the convention in Featherstone’s book as defined in Table A.4 and Section 2.8. If you have two frames A and B and XT the spatial transform from A to B, then XT.E is the rotation matrix that transforms 3d vectors from A to B. In Featherstone’s book you first translate, then rotate.
C++版本的测试代码:
/*
* RBDL - Rigid Body Dynamics Library
* Copyright (c) 2011-2016 Martin Felis <martin@fysx.org>
*
* Licensed under the zlib license. See LICENSE for more details.
*/
#include <iostream>
#include <rbdl/rbdl.h>
using namespace RigidBodyDynamics;
using namespace RigidBodyDynamics::Math;
int main (int argc, char* argv[]) {
//rbdl_print_version();
Model* iiwa_14 = NULL;
unsigned int iiwa_link_id[7];
Body iiwa_link[7];
Joint iiwa_joint[7];
iiwa_14 = new Model();
iiwa_14->gravity = Vector3d (0., 0., -9.81);
iiwa_link[0] = Body(4., Vector3d (0., -0.03, 0.12), Vector3d (0.1, 0.09, 0.02));
iiwa_link[1] = Body(4., Vector3d (0.0003, 0.059, 0.042), Vector3d (0.05,0.018,0.044));
iiwa_link[2] = Body(3., Vector3d (0., 0.03, 0.13), Vector3d (0.08,0.075,0.01));
iiwa_link[3] = Body(2.7, Vector3d (0., 0.067, 0.034), Vector3d (0.03,0.01,0.029));
iiwa_link[4] = Body(1.7, Vector3d (0.0001, 0.021, 0.076), Vector3d (0.02,0.018,0.005));
iiwa_link[5] = Body(1.8, Vector3d (0., 0.0006, 0.0004), Vector3d (0.005,0.0036,0.0047));
iiwa_link[6] = Body(0.3, Vector3d (0., 0., 0.02), Vector3d (0.001,0.001,0.001));
for(int i = 0; i <7; i++)
{
iiwa_joint[i] = Joint(JointTypeRevoluteZ);
}
iiwa_link_id[0] = iiwa_14->AddBody(0, Xtrans(Vector3d(0., 0., 0.1575)), iiwa_joint[0], iiwa_link[0]);
iiwa_link_id[1] = iiwa_14->AddBody(iiwa_link_id[0],
SpatialTransform(Matrix3d(-1.,0,0, 0,0,1., 0,1.,0), Vector3d(0., 0., 0.2025)), iiwa_joint[1], iiwa_link[1]);
iiwa_link_id[2] = iiwa_14->AddBody(iiwa_link_id[1],
SpatialTransform(Matrix3d(-1.,0,0, 0,0,1., 0,1.,0), Vector3d(0., 0.2045, 0.)), iiwa_joint[2], iiwa_link[2]);
iiwa_link_id[3] = iiwa_14->AddBody(iiwa_link_id[2],
SpatialTransform(Matrix3d(1.,0,0, 0,0,1., 0,-1.,0), Vector3d(0., 0., 0.2155)), iiwa_joint[3], iiwa_link[3]);
iiwa_link_id[4] = iiwa_14->AddBody(iiwa_link_id[3],
SpatialTransform(Matrix3d(-1.,0.,0., 0.,0.,1., 0.,1.,0.), Vector3d(0., 0.1845, 0.)), iiwa_joint[4], iiwa_link[4]);
iiwa_link_id[5] = iiwa_14->AddBody(iiwa_link_id[4],
SpatialTransform(Matrix3d(1.,0,0, 0,0,1., 0,-1.,0), Vector3d(0., 0., 0.2155)), iiwa_joint[5], iiwa_link[5]);
iiwa_link_id[6] = iiwa_14->AddBody(iiwa_link_id[5],
SpatialTransform(Matrix3d(-1.,0,0, 0,0,1., 0,1.,0), Vector3d(0., 0.0810, 0.)), iiwa_joint[6], iiwa_link[6]);
VectorNd Q = VectorNd::Zero (iiwa_14->dof_count);
VectorNd QDot = VectorNd::Zero (iiwa_14->dof_count);
VectorNd QDDot = VectorNd::Zero (iiwa_14->dof_count);
Q << 0.234, 0.543, 0.32, 0.521, 1.32, 1.75, 1.2;
QDot << 0.8828 * 30, 0.9137 * 30, 0.5583 * 30, 0.5989 * 30, 0.1489 * 30, 0.8997 * 30, 0.4504 * 30;
QDDot << 0.9718 * 30, 0.9880 * 30, 0.8641 * 30, 0.3889 * 30, 0.4547 * 30, 0.2467 * 30, 0.7844 * 30;
VectorNd Tau = VectorNd::Zero (iiwa_14->dof_count);
// for(int i = 0 ;i < 7 ; i++)
// {
// std::cout << CalcBodyToBaseCoordinates(*iiwa_14, Q, i+1, Vector3d(0., 0., 0.), true) << std::endl;
// std::cout << CalcBodyWorldOrientation(*iiwa_14, Q, i+1, true) << std::endl;
// }
InverseDynamics(*iiwa_14,Q, QDot, QDDot, Tau );
std::cout << Tau.transpose() << std::endl;
// ForwardDynamics (*iiwa_14, Q, QDot, Tau, QDDot);
// std::cout << QDDot.transpose() << std::endl;
delete iiwa_14;
return 0;
}
输出:
[ 1173.0, 28.6, -384.5, -203.6, 14.13, 8.318, -0.7227]
小结
其实上述过程还是历经了一些bug的,比如惯性张量抄错了一位小数…导致结果差很多(加速度和速度比较大,所以惯量的影响比较明显)。再然后就是FeatherStone的特色符号定义了,不过明确了接口,用起来问题就不大。