Ch5-Velocity Kinematics and Statics
Summary:
- 感觉入门的关节在于第三章的twist和wrench,之后的运动学和动力学都是以此为基础的。
- 理解了screw axis就很容易理解为什么要把velocity kinematics单独拿出来讲,并且雅克比矩阵也能很方便的从关节速度映射到末端的速度。
- 静力和力矩的映射也可以用雅克比矩阵反映。
雅克比的概念
正运动学写作:
\[x(t)=f(\theta(t))\]从\theta向量 转到 末端空间的位置向量x:
\[\dot x=\frac{\partial f(\theta)}{\partial \theta} \frac{d\theta(t)}{dt}=\frac{\partial f(\theta)}{\partial \theta} \dot{\theta} \\ =J(\theta) \dot \theta \\ J(\theta)\in \R^{m\times n}, x\in R^{m}, \theta \in R^{n}\]所谓的雅克比矩阵就是将角度向量的微分转化到位置向量的微分。
看图说话:
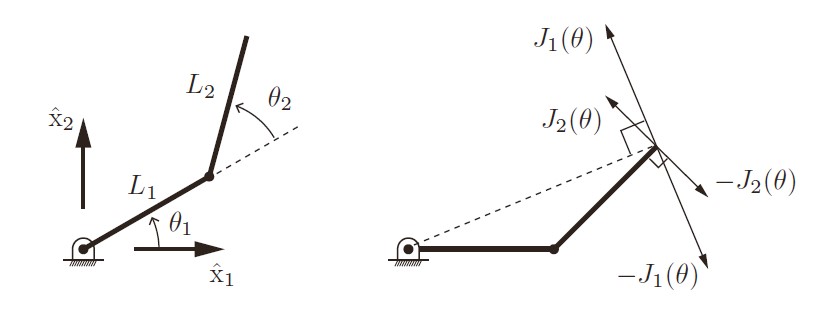
可以很形象的阐述雅克比矩阵在映射关节角速度和末端速度的关系了。J1和J2分别代表\theta1 和\theta2速度对末端速度的贡献,相当于末端速度的基向量,所谓出现奇异值或者冗余无非是雅克比矩阵降秩和线性相关但是维数足够。
这里会有一个很有意思的转换图,从关节空间到末端的工作空间,有速度之间的映射,同时也有静力之间的映射。
一种假设是所有关节的速度平方和确定,也就是速度空间是个球,那么映射到末端的速度空间应该是一个椭球,具体的形状就和雅克比矩阵的特征值会有很大的关系。同时也认为力矩的空间也是个球的话(虽然没什么道理),映射到末端力的空间也会是个椭球,但是因为虚功原理,速度和力应该是对偶的,这样会出现末端速度范围大的方向,对应的力的范围会比较小。
一个例子是人的手水平伸直的时候,提个水桶会很费劲(力不够),但是垂直方向的速度可以很大。相反(vice versa),水平方向几乎没有任何速度,但是能够承受很大的力。
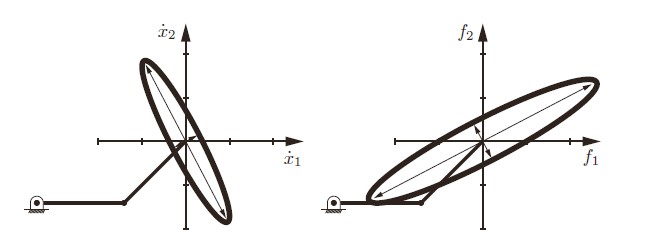
到这里还是前言部分,引出之后利用Ch3,4的screw计算Jacobian。顺带提一嘴力矩到力的关系推导:
\[power \to f_{tip}^Tv_{tip}=\tau^T \dot{\theta} \\ f_{tip}^TJ(\theta)\dot{\theta}=\tau^T \dot{\theta} \\ \tau = J^T(\theta) f_{tip}\]如果J满秩并且是个方阵的话就能求逆啦~得到f映射到力矩的关系,如果J^T满秩但不是方阵(高矩阵),对应冗余,存在零空间。
机械臂的Jacobian
开始正经讲jacobian了,对于给定的关节角和机械臂构位,关节角速度和对应末端的速度是线性映射的关系,首先我们可以选一个坐标系来描述末端的速度,这里很自然的就会用学过的twist(6D),只不过每个screw axes不再是根据初始0度的构位,而是和当前关节角有关系。
对应前面的两种FK的算法,space FK和 body FK,这里也有两种jacobian:
Space Jacobian
沿用twist的概念,对open chain的关节速度和末端twist建立映射。
还记得计算末端T的公式么?
\[T(\theta,...,\theta_{n-1},\theta_{n})=e^{[S_1]\theta_1}...e^{[S_{n-1}]\theta_{n-1}}e^{[S_n]\theta_n}M\]然后就是利用李代数性质的时候了:
\[[\mathcal{V}_s]=\dot{T} T^{-1},~d(e^{A\theta})/dt=Ae^{A\theta}\dot{\theta}\\ 全微分: \dot T= (\frac{d}{dt}e^{[S_1]\theta_1})...e^{[S_n]\theta_n}M + e^{[S_1]\theta_1}(\frac{d}{dt}e^{[S_2]\theta_2})...e^{[S_n]\theta_n}M + ... \\ = [\mathcal{S}_1]\dot{\theta}_1e^{[S_1]\theta_1}...e^{[S_n]\theta_n}M + e^{[S_1]\theta_1}[\mathcal{S}_2]\dot{\theta}_2e^{[S_2]\theta_2}...e^{[S_n]\theta_n}M +... \\ T^{-1} = M^{-1} e^{-[S_n]\theta_n}...e^{-[S_1]\theta_1} \\ \to [\mathcal{V}_s]=[\mathcal{S}_1]\dot{\theta_1} + e^{[S_1]\theta_1}[\mathcal{S}_2]e^{-[S_1]\theta_1}\dot{\theta}_2 + e^{[S_1]\theta_1}e^{[S_2]\theta_2}[\mathcal{S}_3]e^{-[S_2]\theta_2}e^{-[S_1]\theta_1}\dot{\theta}_3 + ... \\ using~~Adjoint \\ \mathcal{V}_s = \underbrace{~~\mathcal{S}_1~~}_{J_{S1}} \dot{\theta}_1 + \underbrace{Ad_{e^{[\mathcal{S}_1]\theta_1}}(\mathcal{S}_2) }_{J_{S2}} \dot{\theta}_2 + \underbrace{Ad_{e^{[\mathcal{S}_1]\theta_1}e^{[\mathcal{S}_2]\theta_2}}(\mathcal{S}_3) }_{J_{S3}} \dot{\theta}_3 + \cdots\\ \to \mathcal{V}_s = \begin{bmatrix}J_{s1} & J_{s2} & \cdots & J_{sn} \end{bmatrix} \begin{bmatrix}\dot{\theta}_1 \\ \dot{\theta}_2 \\ \vdots \\ \dot{\theta}_n \end{bmatrix} =J_s(\theta)\dot{\theta}\]从公式中拆分Js的每一列,可以发现分别是上一个link局部坐标系下转换到space下的screw轴:
\[J_{s_i}=Ad_{T_{i-1}}(S_i),T_{i-1}=e^{[\mathcal{S}_1]\theta_1}\cdots e^{[\mathcal{S}_{i-1}]\theta_{i-1}}\]换句话说就是当前的joint的screw轴在固定坐标系下的表达(和前i-1个关节有关),这也是对于一些简单构型的串联机械臂可以直接看出雅克比矩阵的原因。
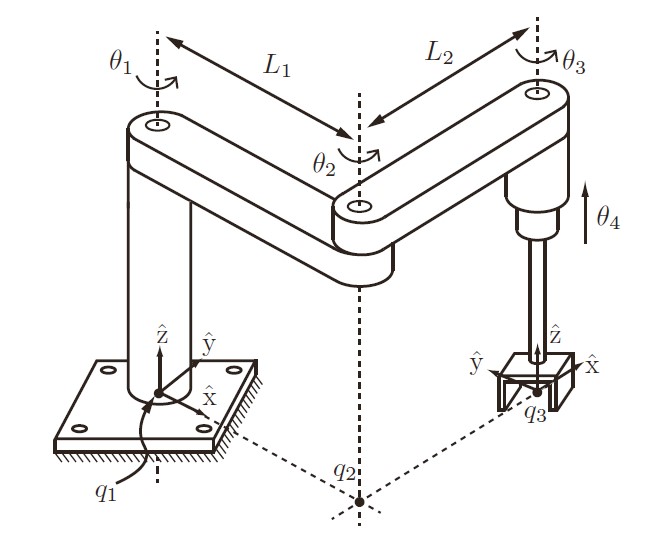
对于该简单构型的机械臂,在当前关节角下,可以直接写出space下的jacobian:
\[J_{s}(\theta)=\begin{bmatrix} 0&0&0&0\\0&0&0&0\\1&1&1&0\\ 0&L_1sin(\theta_1)&L_1s_1+L_2s_{12}&0\\ 0&-L_1cos(\theta_1)&-L_1c_1-L_2c_{12}&0\\ 0&0&0&1 \end{bmatrix}\]从Jacobian矩阵中也能分析出末端自由度为4,并且z方向的运动之和j4有关,而xy的平动和j1~3有关,只有z的角速度和j1~3有关。
Body Jacobian
对于body坐标系下算雅克比矩阵,只需要换个顺序:
\[[\mathcal{V}_b]=T^{-1}\dot{T}\\ T(\theta)=Me^{\mathcal{B}_1 \theta_1}...e^{ \mathcal{B}_n\theta_n} \\ \to \\ [\mathcal{V}_b]=[\mathcal{B}_n]\dot{\theta}_{n}+ e^{-[\mathcal{B}_n]\theta_n}[\mathcal{B}_{n-1}]e^{[\mathcal{B}_n]\theta_n}\dot{\theta}_{n-1}+... +e^{-[\mathcal{B}_n]\theta_n} \cdots e^{-[\mathcal{B}_2]\theta_2}[\mathcal{B}_{1}] e^{[\mathcal{B}_2]\theta_2} \cdots e^{[\mathcal{B}_n]\theta_n}\dot{\theta}_{1} \\ \to \\ \mathcal{V}_b = \underbrace{~~\mathcal{B}_n~~}_{J_{bn}} \dot{\theta}_{n} + \underbrace{Ad_{e^{[\mathcal{B}_n]\theta_n}}(\mathcal{B}_{n-1}) }_{J_{b,{n-1}}} \dot{\theta}_{n-1} + \underbrace{Ad_{e^{[\mathcal{B}_{n}]\theta_n}e^{[\mathcal{B}_{n-1}]\theta_{n-1}}}(\mathcal{B}_{n-2}) }_{J_{b,{n-2}}} \dot{\theta}_{n-2} + \cdots\\ \to \\ \mathcal{V}_b = \begin{bmatrix}J_{b1} & J_{b2} & \cdots & J_{bn} \end{bmatrix} \begin{bmatrix}\dot{\theta}_1 \\ \dot{\theta}_2 \\ \vdots \\ \dot{\theta}_n \end{bmatrix} =J_b(\theta)\dot{\theta} \\\]其中第i个joint的转轴相对于末端坐标系的screw和i+1~n个joint的关节角有关:
\[J_{bi}(\theta)=Ad_{e^{-[\mathcal{B_n}]\theta_n} \cdots e^{-[\mathcal{B_{i+1}}]\theta_{i+1}}}(\mathcal{B_i})\]这个理解起来也很容易,因为就是base的jacobian所以肯定从base开始往前推。
Space和Body Jacobian的关系
这个关系很容易推导…
从s到b的坐标变换:
\[\mathcal{V_s}=Ad_{T_{sb}}(\mathcal{V_b}) = J_s(\theta)\dot{\theta} \\ [Ad_X][Ad_Y]=[Ad_{XY}] \\ Ad_{T_{bs}}(Ad_{T_{sb}}(\mathcal{V}_b)) = Ad_{T_{bs}T_{sb}}(\mathcal{V}_b)=\mathcal{V}_b=Ad_{T_{bs}}(J_s(\theta)\dot{\theta})=Ad_{T_{bs}}(J_s(\theta))\dot{\theta} \\ \mathcal{V}_b=J_b(\theta)\dot{\theta}\\ \to J_b(\theta)=Ad_{T_{bs}}(J_s(\theta))=[Ad_{T_{bs}}]J_s(\theta)\\ \to J_s(\theta)=Ad_{T_{sb}}(J_b(\theta))=[Ad_{T_{sb}}]J_b(\theta)\\\]其他形式的雅克比
这里的两种形式指的是末端速度的表达方式不同,如果用twist表示,那么就是之前推导的geometric jacobian;如果用其他坐标系定义q,那么末端速度则是\dot{q},此时的速度关系矩阵叫做analytic jacobian。
举个例子: 末端速度用指数坐标表示旋转的jacobian和geometric的关系:
\[\mathcal{V}_b=\begin{bmatrix} \omega_b \\ v_b \end{bmatrix} = J_b(\theta)\dot{\theta}=\begin{bmatrix} J_\omega{(\theta)} \\ J_v(\theta) \end{bmatrix}\dot{\theta} \\ q = [r;x], r=\hat{\omega}\theta\in \R^3,x\in\R^3 \\ \dot{x}=R_{sb}(\theta)v_b=R_{sb}(\theta)J_v(\theta)\dot{\theta} =e^{[\hat{\omega}]\theta}J_v(\theta)\dot{\theta} \\ \dot{r}=A^{-1}(r)\omega_b=A^{-1}(r)J_\omega(\theta)\dot{\theta}\\ \to \dot{q} = \begin{bmatrix} \dot{r} \\ \dot{x}\end{bmatrix} =\begin{bmatrix} A^{-1}(r) & 0\\0 & R_{sb}(\theta)\end{bmatrix} \begin{bmatrix} \omega_b \\ v_b \end{bmatrix}\]因此两种雅克比之间相差的也仅是一个对角块矩阵(速度和角速度独立)
Inverse Velocity Kinematics
之前我们是输入每个关节的角速度,输出末端的twist运动,但是我们一般面对的问题是给定末端的twist运动,要求每个关节角速度。
- 最平凡的:Jacobian是方阵,并且可逆,皆大欢喜。
- Jacobian不可逆(不是方阵或者降秩),涉及到广义逆的问题,特殊的是当joint数量大于6时,也叫做redundant冗余,期望的twist运动对于关节来说相当于6维的约束,剩下的自由度并不会影响末端的运动,在J零空间里做规划是非常值得讨论的。(具体在Ch6.3里会详细的展开)
力的Jacobian
用关节力矩到末端力的Jacobian也可以得出类似的结论:
\[\tau^T \dot{\theta}=\mathcal{F}^T_b \mathcal{V}_b = \mathcal{F}^T_b J_b(\theta)\dot{\theta} \\ \to \tau = J_b^T(\theta) \mathcal{F}_b = J_s^T(\theta)\mathcal{F}_s\]此时都是静力分析,末端加载一个wrench为-F就和机械臂末端的wrench抵消,并且能够算出此时各个关节需要输出多大的力矩使得末端达到平衡。(这里不考虑机械臂自重带来的重力补偿问题)
\[\mathcal{F}_s=J^{-T}(\theta)\tau\]相反,如果已知各个关节力矩为\tau,也可以求出此时末端负载大小,也会遇到jacobian是否奇异,病态的问题。
当N>6,机械臂可以在末端不动的情况下,产生link的运动,此时要考虑更多动态的问题。
当N<6,机械臂在6-n的wrench方向上无法产生力(或者说在结构允许下可以抵抗任意大的力),这是力的jacobian的零空间决定的:
\[Null(J^T(\theta))=\{ \mathcal{F}|J^T(\theta)\mathcal{F}=0\}, J^T\in\R^{N\times6}\]小例子:一个自由度的转轴门,可以抵抗零空间内任意大小的作用力,因为无法反应到关节力矩上去。
奇异分析(Singularity Analysis)
机械臂的奇异性之和当前构型有关,和jacobian选取在{s}还是{b}还是其他什么frame没有关系,这个从
\[rank{J_s(\theta)} = rank(J_b(\theta))\\ \dot{T'}(T')^-1=(\dot T Q)(Q^{-1}T^{-1})=\dot{T}T^{-1}\]中就可以看出。分析奇异主要是看各个子列的是否线性无关。
可操作度(Manipulability)
因为奇异性是bool变量,只有奇异和非奇异,类比矩阵论中对矩阵病态程度的描述(矩阵条件数),可操作度也是对奇异性的一种度量,能够反映近似奇异的病态构型。
对于jacobian,其数值稳定性不仅体现在是否奇异上,更体现在特征值之间的大小差异上。如果某些维度的特征值相对很小,也是近似奇异或者病态的。矩阵理论中JJ^T的特征值可以定义一个m维的超椭球满足:
换个想法,末端空间的运动是每个关节运动乘以Jacobian的子列得到的各个方向运动的线性空间,那么这个线性空间无论是否线性相关或者病态,总是对应会有一组线性无关的基向量和对应的特征值
\[\dot{q}^TA^{-1}\dot{q} = 1\]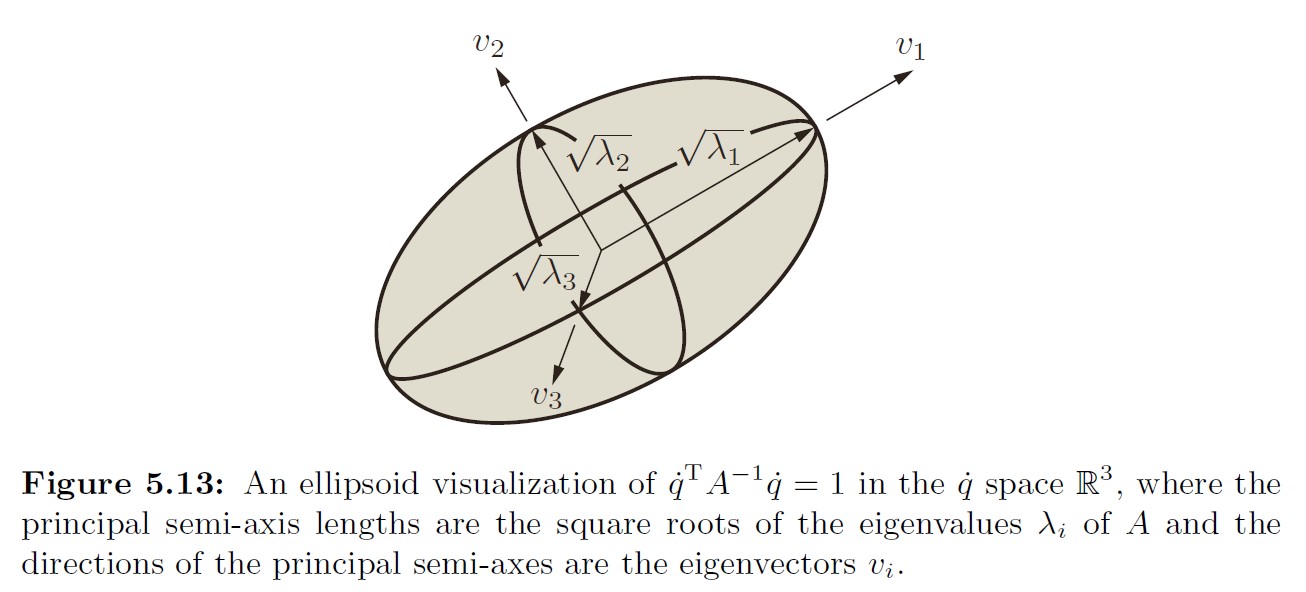
椭球的超体积正比于各个半长轴长度,也即:
\[V \propto \sqrt{\lambda_1 \lambda_2 \cdots \lambda_n}= \sqrt{det(A)} = \sqrt{det(JJ^T)}\]又因为Jacobian可以分为角速度和线速度的Jacobian,利用分块矩阵性质,A矩阵最终也是对角的分块矩阵(Jw*Jtheta = 0?)因此,可以在角速度和线速度两个R3空间内画出对应的Jacobian椭球,每个轴的方向就是对应特征向量的方向,而长度对应该方向上\dot{q}的大小,越大,可以认为该方向速度变化范围也越大,如果某个方向的椭球范围很小,这说明这里近似奇异了。
理想的操作空间应该是各向同性的,也就是椭球最好近似为一个球,这样就不会出现某个方向的运动受限的情况,然而实际情况并不会那么理想,定义最大主轴和最小主轴的比值就得到了A的一个可操作度的度量。
\[\mu_1(A) = \frac{\sqrt{\lambda_{max}(A)}}{\sqrt{\lambda_{min}(A)}} \geq 1\]该度量越接近1,操作度越好(各方向越均匀),类似的概念在矩阵中叫做条件数,是A的最大特征值和最小特征值的比值:
\[\mu_2(A)=cond(A)=|\frac{\lambda_{max}}{\lambda_{min}}| \geq 1\]当然如果各个方向都差不多很小的话也没什么卵用,这是就需要对体积也有一个刻画:
\[\mu_3(A)=\sqrt{det(A)}\]再提一嘴,因为之前假设\dot{\theta} 范数为1,在关节力和末端力的关系里,通常假设关节输出的力大小一定,那么我们就得到:
\[1 = f^TJJ^Tf=f^TB^{-1}f=f^T(A^{-1})^{-1}f \\ \to \mu_3(A) \mu_3(B) = 1 \\ \mu_1(A) = \mu_1(B), \mu_2(A) = \mu_2(B)\]因此末端wrench的两个椭球的半长轴是速度半长轴的倒数,但是方向是一致的(符合我们对功率的认识)